
Introducción
El objetivo principal de esta breve discusión es proporcionar los principios que guían la selección de soportes antivibratorios, utilizados para el aislamiento de sistemas o partes de los mismos, en aquellos casos en los que también se debe considerar el esfuerzo sísmico. Esto también implica aclarar un concepto erróneo pero muy común, a saber, que existen soportes antivibratorios utilizados para el aislamiento de sistemas que, al igual que los estructurales utilizados en el campo de la construcción, son capaces de atenuar las aceleraciones sísmicas. En este texto, no hay un análisis en profundidad relacionado con las tensiones sísmicas ni con los métodos de cálculo y fórmulas relacionadas que deben evaluarse para el cumplimiento de los diversos códigos antisísmicos internacionales.
La selección de soportes antivibratorios
The primary need is the same as for the selections for isolation from vibrations, produced by the equipment or the environment external to it, or to «cut» the medium / high frequency excitations typical of these spectra (25 ÷ 50H z) . At the same time, the main requirement common to all international anti-seismic codes must be met, namely that the resistance of the mechanical constraint must be guaranteed, during and after the seismic event.
During the earthquake, in almost all cases, the anti-vibration support responds in resonance to the earthquake. This involves an amplification of accelerations and displacements, with a factor of 2 ÷ 10 times. Seismic excitation has a spectrum with greater amplitudes at low frequencies (2 ÷ 10 H z).
With a mechanical mass-spring-damper system (with 1 degree of freedom), the isolation of a certain portion of the spectrum is obtained by positioning the natural frequency at low / very low frequency. This is achieved by appropriately selecting the stiffness of the anti-vibration support. However, it is also necessary that the frame / structure of the insulated mass be very rigid in each orthogonal direction, so that the e ective mass of the 1st mode of the system, once mounted on the anti-vibration supports, is equal to almost all the suspended equipment. . If this were not the case, we would find ourselves in the presence of higher modes with significant mass participation.
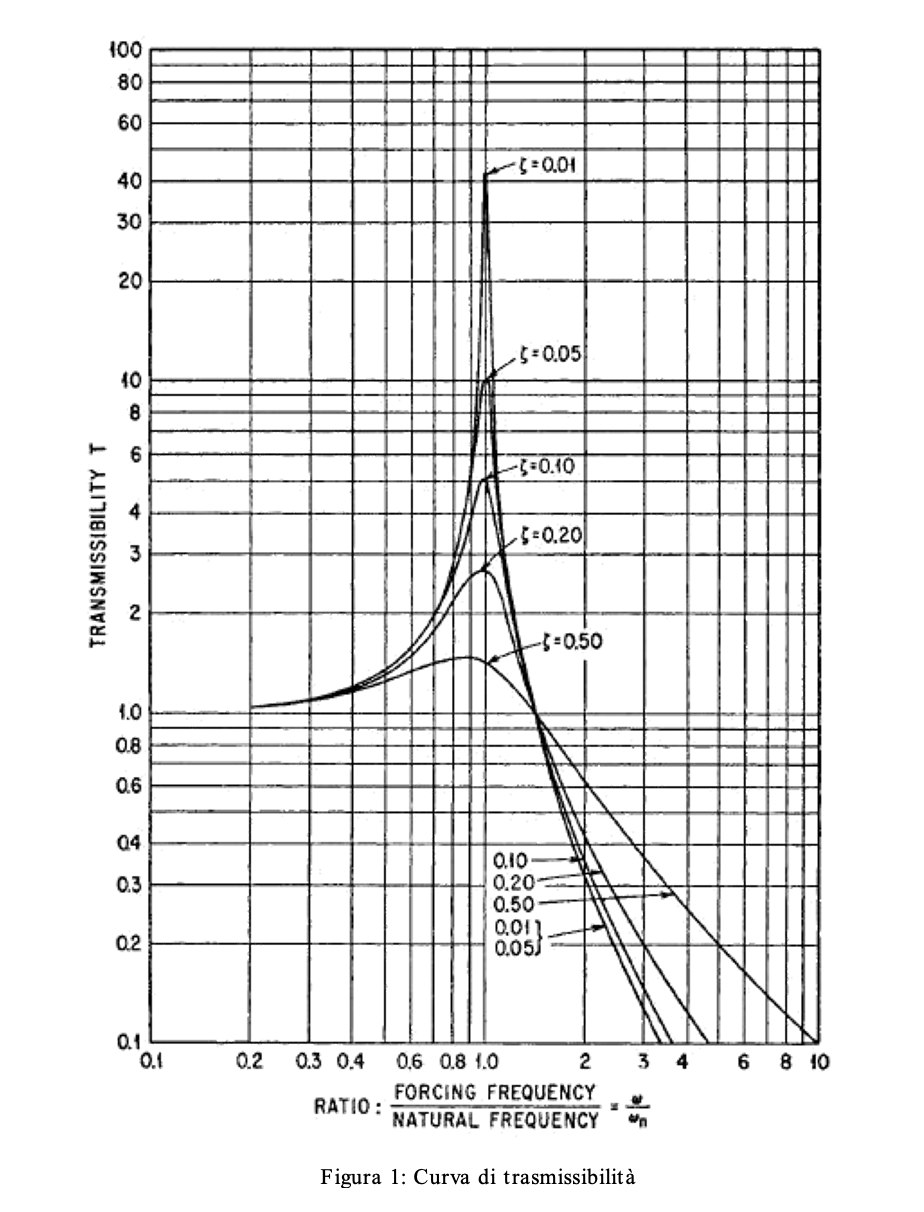
The choice of anti-vibration mounts is obtained from the transmissibility curve, the shape of which
typical is visible in Figure 1 – taken from Harris’s Shock and Vibration Handbook, 5th edition (2002), compared with the spectra of excitations, both for normal conditions
exercise for both the earthquake.
This curve highlights the presence of two zones in the frequency range, with opposite effects from the point of view of isolation or amplification of the stress:
1. Excitations with frequencies lower than √ 2 times the natural frequency are amplified
2. excitations with frequencies higher than √ 2 times the natural frequency are attenuated.
Also note the different damping weight in these two areas:
1.In the amplification zone, an increase in damping corresponds to an e ect
beneficial with the reduction of amplification
2.In the attenuation zone, an increase in damping corresponds to an e ect
negative with the reduction of insulation.
La necesidad primaria es la misma que para las selecciones para el aislamiento de vibraciones, producidas por el equipo o el ambiente externo a él, o para «cortar» las excitaciones de media/alta frecuencia típicas de estos espectros (25 ÷ 50H z). Al mismo tiempo, se debe cumplir con el principal requisito común a todos los códigos antisísmicos internacionales, a saber, que se debe garantizar la resistencia de la restricción mecánica, durante y después del evento sísmico.
Durante el sismo, en casi todos los casos, el soporte antivibratorio responde en resonancia al sismo. Esto implica una amplificación de aceleraciones y desplazamientos, con un factor de 2 ÷ 10 veces. La excitación sísmica tiene un espectro con mayores amplitudes a bajas frecuencias (2 ÷ 10 H z).
Con un sistema mecánico masa-resorte-amortiguador (con 1 grado de libertad), el aislamiento de una determinada porción del espectro se obtiene posicionando la frecuencia natural en baja/muy baja frecuencia. Esto se consigue seleccionando adecuadamente la rigidez del soporte antivibratorio. Sin embargo, también es necesario que el marco/estructura de la masa aislada sea muy rígido en cada dirección ortogonal, de manera que la masa efectiva del 1er modo del sistema, una vez montado sobre los soportes antivibratorios, sea igual a casi todo el equipo suspendido. . De no ser así, nos encontraríamos en presencia de modalidades superiores con una importante participación masiva.
La elección de los soportes antivibratorios se obtiene a partir de la curva de transmisibilidad, cuya forma
típico es visible en la Figura 1 – tomado de Harris’s Shock and Vibration Handbook, 5th edition (2002), comparado con los espectros de excitaciones, ambos para condiciones normales
Ejercicio para tanto el terremoto.
Esta curva destaca la presencia de dos zonas en el rango de frecuencia, con efectos opuestos desde el punto de vista del aislamiento o amplificación del estrés:
1. Se amplifican excitaciones con frecuencias inferiores a √ 2 veces la frecuencia natural
2. Se atenúan las excitaciones con frecuencias superiores a √ 2 veces la frecuencia natural.
Tenga en cuenta también el diferente peso de amortiguación en estas dos áreas:
1.En la zona de amplificación, un aumento de la amortiguación corresponde a un efecto
beneficioso con la reducción de la amplificación
2.En la zona de atenuación, un aumento de la amortiguación corresponde a un efecto
negativo con la reducción del aislamiento.
Si bien en la siguiente discusión se tomará en consideración la amortiguación como parámetro de selección/dimensionamiento, en realidad no está disponible ya que es una característica intrínseca de la serie de soportes antivibratorios, prácticamente fijada cuando la rigidez y las capacidades de carga variar.
Volviendo a los conceptos que acabamos de expresar, la elección de los parámetros dinámicos (rigidez, amortiguamiento y recorrido disponible, que se tratará en detalle a continuación), debe tener en cuenta solicitudes contradictorias:
• para obtener un corte efectivo de las vibraciones típicas en condiciones normales de funcionamiento (por encima de 25 Hz), se requieren bajas frecuencias naturales y bajos valores de amortiguamiento
• para evitar o, al menos, limitar la excitación de resonancia en respuesta al terremoto,
se necesitan frecuencias naturales más altas (para buscar un mayor desacoplamiento) y mayor amortiguamiento, para contener el factor de amplificación.
Sin embargo, cabe señalar que se requieren grandes desplazamientos para que los sistemas altamente amortiguados sean efectivos. Si bien los desplazamientos de gran amplitud están ciertamente relacionados con eventos sísmicos, el desplazamiento máximo debe mantenerse bajo control y verificar que no sea mayor que el disponible del soporte antivibratorio.
Superar esta disponibilidad provoca choques de final de carrera que, además de los posibles problemas de resistencia estructural, podrían introducir excitaciones de alta frecuencia. Se pueden minimizar evitando la presencia de finales de carrera rígidos.
En definitiva, es recomendable, en términos generales, seleccionar soportes antivibratorios
que crean una suspensión con frecuencia natural superior a 10 Hz, excepto en el caso
en los que los apoyos no tengan un amortiguamiento crítico superior al 20% (como aquellos con cuerdas
metal), ya que garantizan una amplificación de resonancia inferior a 3 veces. En todos los casos, se debe evaluar cuidadosamente que la carrera disponible sea compatible con los desplazamientos máximos esperados.
Author: Ing. William Prina
Otras noticias


Soportes antivibratorios con retención antisísmica



